Pensamiento Matemático

El pensamiento matemático es un recurso sociocognitivo que involucra diversas actividades desde la ejecución de operaciones y el desarrollo de procedimientos y algoritmos hasta los procesos mentales abstractos que se dan cuando el sujeto participa del quehacer matemático, pretende resolver problemas, usar o crear modelos, y le dan la posibilidad de elaborar tanto conjeturas como argumentos; organizar, sustentar y comunicar sus ideas.

Los recursos aportados a la formación del sujeto desde el pensamiento matemático son variados y abarcan técnicas, un lenguaje formal, procesos de pensamiento (entre los que destacan observar, intuir, conjeturar y argumentar), diversos métodos y heurísticas para la solución de problemas, la adquisición de habilidades para modelar una situación o fenómeno, formas de simbolizar, organizar y comunicar información, entre otros. También corresponde a esta área, el establecimiento de procesos para la negociación de significados y para comunicar la experiencia vivida.

El pensamiento matemático además busca que las y los estudiantes del bachillerato logren comprender mejor otras áreas de conocimiento y la aplicación del mismo en la toma de decisiones razonadas y en la valoración de la matemática por su belleza, utilidad y como un factor fundamental en la creación de su proyecto de vida.

Así se llevará al estudiantado del nivel medio superior a desarrollar procesos de razonamiento tanto lógicos como intuitivos, a desarrollar la creatividad y la imaginación, la curiosidad y la reflexión con la intención de conducirlo a un mayor nivel intelectual para fomentar el aprendizaje permanente y qué éste sea gestionarlo por el propio sujeto.

El pensamiento matemático, en el MCCEMS, posibilita:

Favorecer en el estudiantado el desarrollo de habilidades relacionadas con la observación, la intuición, la capacidad de conjeturar, la argumentación, la comunicación y socialización de inquietudes intelectuales y soluciones a problemas, así como la descripción de fenómenos o situaciones mediante el empleo del lenguaje matemático.
Recuperar una perspectiva histórico-filosófica para ver a la matemática a
partir de los contextos que dieron origen a los conceptos y procedimientos, de la integración de procesos de abstracción, argumentación y otros, dando un enfoque amplio contrario al enfoque mecanicista que anula la relevancia de la matemática.
Responder a motivaciones que pueden estar en el ambiente natural, social, cultural o en el sujeto pensante, para ampliar la visión de la matemática considerando su papel transformador, su dimensión cultural e intelectual que favorezca la formación integral del ser humano.
Dar un sentido holístico a la formación matemática en la EMS para que el estudiantado alcance una educación de calidad, que incluya contenidos relevantes, actividades pertinentes y retadoras para lograr que le dé seguridad para tomar decisiones, favorezca una postura crítica y un estado emocional que lo impulse hacia el aprendizaje permanente y desarrolle una postura crítica en un marco de respeto a la condición y dignidad humana.
Incorporar una visión centrada en el estudiante de tal forma que la articulación de saberes, conocimientos y habilidades tenga como eje director el progreso del estudiantado, respetando siempre la coherencia y consistencia de la disciplina.

Consulta el documento oficial expedido por la Secretaría de Educación Pública aquí.

Aprendizajes de Trayectoria

El perfil de egreso de Pensamiento Matemático se conforma por los siguientes aprendizajes de trayectoria:

AT1. Valora la aplicación de procedimientos automáticos y de algoritmos para anticipar, encontrar y validar soluciones a problemas (matemáticos, de las ciencias naturales, experimentales y tecnología, sociales, humanidades y de la vida cotidiana).
AT2. Adapta procesos de razonamiento matemático que permiten relacionar información y obtener conclusiones de problemas (matemáticos, de las ciencias naturales, experimentales y tecnología, sociales, humanidades, y de la vida cotidiana).
AT3. Modela y propone soluciones a problemas (matemáticos, de las ciencias naturales, experimentales y tecnología, sociales, humanidades y de la vida cotidiana) empleando lenguaje y técnicas matemáticas.
AT4. Explica la solución de problemas en el contexto que le dio origen, empleando lenguaje matemático y lo valora como relevante y cercano a su vida.

Organización Curricular

La organización curricular de Pensamiento Matemático se compone de tres programas de estudio:

Unidades de Aprendizaje Curricular	Semestre	Horas semanales			Horas semestrales			Créditos
Unidades de Aprendizaje Curricular	Semestre	MD	EI	Total	MD	EI	Total	Créditos
Pensamiento Matemático I	Primero	4	1	5	64	16	80	8
Pensamiento Matemático II	Segundo	4	1	5	64	16	80	8
Pensamiento Matemático III	Tercero	4	1	5	64	16	80	8

Notas:

La estructura por semestre puede variar de acuerdo con el mapa curricular de cada servicio educativo.
MD = Mediación docente
EI = Estudio independiente

Metas de Aprendizaje

Una meta de aprendizaje enuncia lo que se pretende que los estudiantes aprendan durante la trayectoria de cada semestre, lo cual permitirá construir de manera continua y eslabonada las estrategias de enseñanza, de aprendizaje y de evaluación para el logro de los aprendizajes de trayectoria.

A continuación se enuncian las metas por semestre, dados los semestres en los que se ha definido una asignatura de Pensamiento Matemático:

Para Pensamiento Matemático se emplean las mismas metas de aprendizaje (en frecuencias diferentes por progresión de aprendizaje) en cada UAC. La única que no se emplea en 1° Semestre es M4.3.

Semestre	Metas de Aprendizaje
1° Semestre	M1.1. Ejecuta cálculos y algoritmos para resolver problemas matemáticos y de otras áreas del conocimiento. M1.2. Analiza los resultados obtenidos al aplicar procedimientos algorítmicos propios del Pensamiento Matemático en la resolución de problemáticas teóricas y de su contexto. M1.3. Comprueba los procedimientos usados en la resolución de problemas matemáticos y de otras áreas del conocimiento, mediante la verificación directa o empleando recursos tecnológicos o la interacción con sus pares. M2.1. Observa y obtiene información de una situación o fenómeno (natural o social) para establecer estrategias o formas de visualización que ayuden a explicarlo. M2.2. Desarrolla la percepción y la intuición para generar una hipótesis inicial ante situaciones que requieren explicación o interpretación. M2.3. Compara hechos, opiniones o afirmaciones categóricas o la posibilidad de ocurrencia de eventos para establecer similitudes y diferencias, organizándolos en formas lógicas o convenientes útiles en la solución de problemas. M2.4. Combina diferentes procesos de razonamiento matemático al plantear un modelo o resolver un problema o una situación o fenómeno natural, experimental o social e interpreta el resultado, la predicción y/o la manera de reducir el nivel de riesgo. M3.1. Selecciona un modelo matemático por la pertinencia de sus variables y relaciones para explicar el fenómeno estudiado en la solución de un problema. M3.2. Construye un modelo con lenguaje matemático y pone a prueba su utilidad para el estudio de un fenómeno (natural o social) o una situación problema. M3.3. Aplica procedimientos, técnicas y lenguaje matemático para la solución de problemas propios del Pensamiento Matemático, de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno. M3.4. Construye y plantea posibles soluciones a problemas de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno, empleando técnicas y lenguaje matemático. M4.1. Describe con sus pares sus conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno. M4.2. Socializa con sus pares conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno.
2° Semestre	M1.1. Ejecuta cálculos y algoritmos para resolver problemas matemáticos y de otras áreas del conocimiento. M1.2. Analiza los resultados obtenidos al aplicar procedimientos algorítmicos propios del Pensamiento Matemático en la resolución de problemáticas teóricas y de su contexto. M1.3. Comprueba los procedimientos usados en la resolución de problemas matemáticos y de otras áreas del conocimiento, mediante la verificación directa o empleando recursos tecnológicos o la interacción con sus pares. M2.1. Observa y obtiene información de una situación o fenómeno (natural o social) para establecer estrategias o formas de visualización que ayuden a explicarlo. M2.2. Desarrolla la percepción y la intuición para generar una hipótesis inicial ante situaciones que requieren explicación o interpretación. M2.3. Compara hechos, opiniones o afirmaciones categóricas o la posibilidad de ocurrencia de eventos para establecer similitudes y diferencias, organizándolos en formas lógicas o convenientes útiles en la solución de problemas. M2.4. Combina diferentes procesos de razonamiento matemático al plantear un modelo o resolver un problema o una situación o fenómeno natural, experimental o social e interpreta el resultado, la predicción y/o la manera de reducir el nivel de riesgo. M3.1. Selecciona un modelo matemático por la pertinencia de sus variables y relaciones para explicar el fenómeno estudiado en la solución de un problema. M3.2. Construye un modelo con lenguaje matemático y pone a prueba su utilidad para el estudio de un fenómeno (natural o social) o una situación problema. M3.3. Aplica procedimientos, técnicas y lenguaje matemático para la solución de problemas propios del Pensamiento Matemático, de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno. M3.4. Construye y plantea posibles soluciones a problemas de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno, empleando técnicas y lenguaje matemático. M4.1. Describe con sus pares sus conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno. M4.2. Socializa con sus pares conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno. M4.3. Organiza los procedimientos empleados en la solución de un problema a través de argumentos formales para someterlo a debate o a evaluación.
3° Semestre	M1.1. Ejecuta cálculos y algoritmos para resolver problemas matemáticos y de otras áreas del conocimiento. M1.2. Analiza los resultados obtenidos al aplicar procedimientos algorítmicos propios del Pensamiento Matemático en la resolución de problemáticas teóricas y de su contexto. M1.3. Comprueba los procedimientos usados en la resolución de problemas matemáticos y de otras áreas del conocimiento, mediante la verificación directa o empleando recursos tecnológicos o la interacción con sus pares. M2.1. Observa y obtiene información de una situación o fenómeno (natural o social) para establecer estrategias o formas de visualización que ayuden a explicarlo. M2.2. Desarrolla la percepción y la intuición para generar una hipótesis inicial ante situaciones que requieren explicación o interpretación. M2.3. Compara hechos, opiniones o afirmaciones categóricas o la posibilidad de ocurrencia de eventos para establecer similitudes y diferencias, organizándolos en formas lógicas o convenientes útiles en la solución de problemas. M2.4. Combina diferentes procesos de razonamiento matemático al plantear un modelo o resolver un problema o una situación o fenómeno natural, experimental o social e interpreta el resultado, la predicción y/o la manera de reducir el nivel de riesgo. M3.1. Selecciona un modelo matemático por la pertinencia de sus variables y relaciones para explicar el fenómeno estudiado en la solución de un problema. M3.2. Construye un modelo con lenguaje matemático y pone a prueba su utilidad para el estudio de un fenómeno (natural o social) o una situación problema. M3.3. Aplica procedimientos, técnicas y lenguaje matemático para la solución de problemas propios del Pensamiento Matemático, de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno. M3.4. Construye y plantea posibles soluciones a problemas de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno, empleando técnicas y lenguaje matemático. M4.1. Describe con sus pares sus conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno. M4.2. Socializa con sus pares conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno. M4.3. Organiza los procedimientos empleados en la solución de un problema a través de argumentos formales para someterlo a debate o a evaluación.

Categorías y Subcategorías

Las categorías de Pensamiento Matemático son 4, las cuales se dividen en 13 subcategorías:

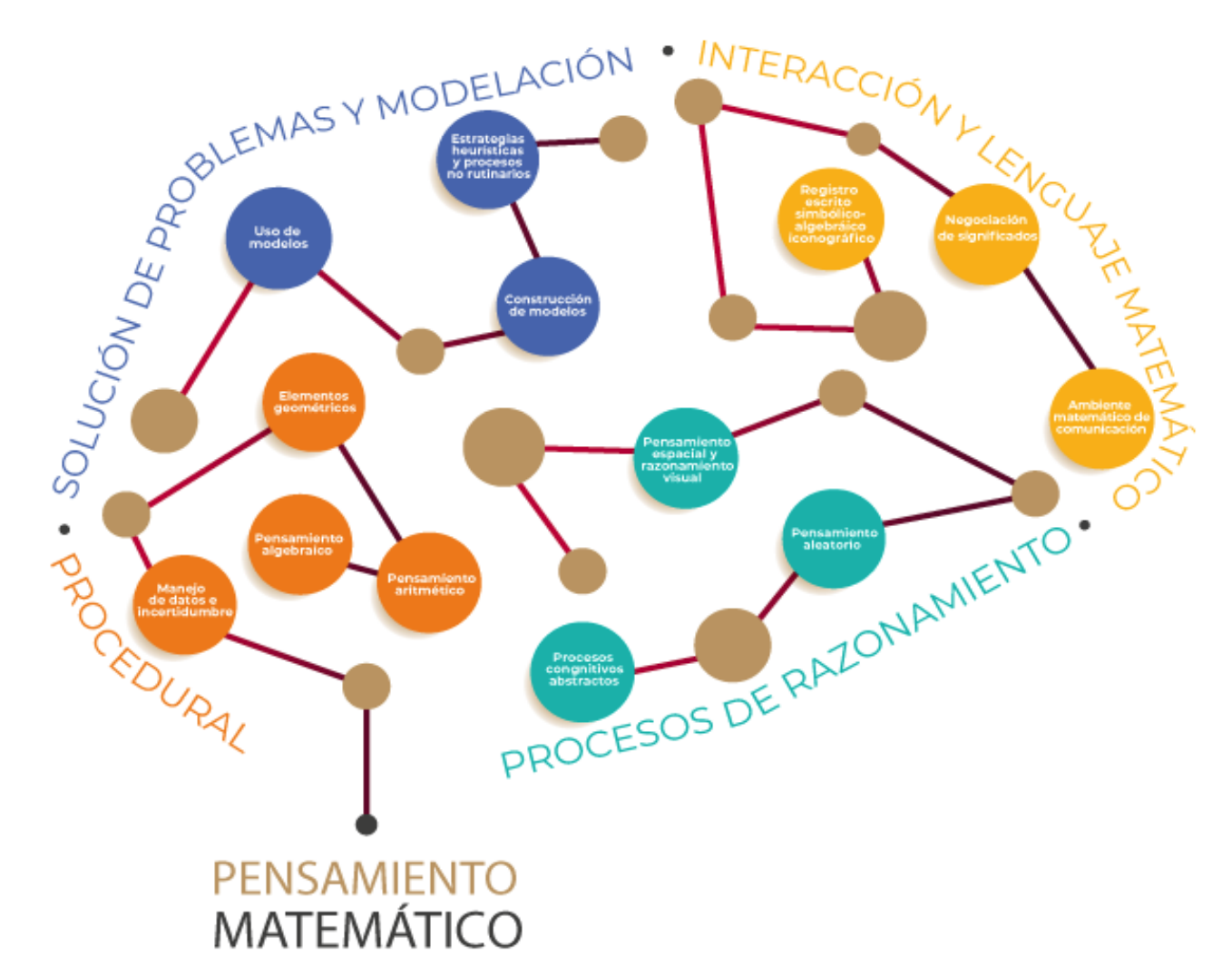
Categoría	Definición	Subcategoría	Definición
Procedural	Se refiere al conjunto de procedimientos matemáticos, algorítmicos y heurísticos, entendidos, como un "saber hacer" automático e inmediato que le posibilita al estudiante dar una respuesta ante un cuestionamiento o situación- problema. Lleva a describir y ejecutar procedimientos matemáticos, en forma sintética o extendida, automatizada o como una secuencia razonada de pasos. En las diferentes áreas de la matemática hay formas de hacer, de resolver, de simplificar, etc., por eso su contenido se vuelve un valioso recurso al emplearlos en la solución de problemas y en la toma de decisiones.	Pensamiento aritmético	Procesos de pensamiento basados en la comprensión del uso y de los significados de los números y de la numeración; el sentido y significado de las operaciones y de las relaciones entre números, y el desarrollo de diferentes técnicas de cálculo y estimación.
		Pensamiento algebraico	Tipo de pensamiento complejo que involucra la comprensión de las relaciones numéricas y funcionales, los patrones, su generalización, incluye el uso de estructuras y símbolos para formalizar abstracciones y generalizaciones.
		Elementos geométricos	Los elementos geométricos consideran puntos, líneas, figuras, planos, espacios, etc. Algunas veces relacionados con propiedades o con sistemas de referencia mediante el uso de coordenadas y/o magnitudes.
		Manejo de datos e incertidumbre	Considera el uso e interpretación de datos y el cálculo de sus posibilidades de ocurrencia. Incluye desde la recolección de datos, la revisión de los términos básicos utilizados en probabilidad y estadística y las formas en que se recolectan datos a partir de una necesidad específica, así como las ventajas de elegir una forma para organizarlos, interpretarlos y utilizarlos en la toma de decisiones en ambientes de incertidumbre.
Procesos de intuición y razonamiento	Conjunto de procesos complejos, que pueden ser de diferente naturaleza ya sea intuitiva o lógica, que permiten relacionar, vincular, comparar y analizar información en forma estructurada, a partir de un conjunto de premisas, establecer conjeturas, diseñar estrategias, elaborar inferencias, obtener resultados o hacer deducciones, construir argumentos, obtener conclusiones, entre otras. Dota de un conjunto de habilidades cognitivas complejas, con las cuales la persona se relaciona u obtiene información mediante las acciones antes mencionadas (intuir, observar, comparar, asociar, analizar, sintetizar, deducir, inducir, generalizar, abstraer, modelar, simbolizar, cuestionar, dudar, elaborar conjeturas) éstas a su vez son detonadoras de otros recursos, útiles a las demás áreas, entre las cuales destacan: resolver, promover la justificación, argumentar, comprobar, validar, etc.	Procesos cognitivos abstractos	Consiste en una forma de pensamiento complejo, representa un avance que se define como un “salto cualitativo” a partir del pensamiento concreto u operatorio. Este pensamiento se caracteriza por la construcción de una serie de razonamientos, mucho más elaborados que se apoyan en estructuras cerebrales, que empiezan a generarse en la adolescencia.
		Pensamiento espacial y razonamiento virtual	El pensamiento espacial se refiere al conjunto de procesos y habilidades visuales que permite al alumnado organizar y controlar información a partir de la manipulación de objetos concretos, con la finalidad de resolver un problema, a veces requiere transformar una representación externa en forma de representación interna esto se identifica como un razonamiento visual, surge como resultado de una compleja actividad mental analítico–sintética que destaca rasgos esenciales de lo que se está viendo y mantiene inhibidos otros que no lo son.
		Pensamiento aleatorio	El razonamiento visual requiere combinar procesos: de análisis, en donde se parcializa al objeto en sus características, y de síntesis, mediante el cual se construye una nueva estructura que se compara con la percepción anterior. El pensamiento aleatorio se apoya directamente en conceptos y procedimientos de la teoría de probabilidades y de la estadística inferencial e indirectamente en la estadística descriptiva y en la combinatoria. Ayuda a buscar soluciones razonables a problemas en los que no hay una solución clara y segura, mediante exploración y la construcción de modelos de fenómenos físicos, sociales o de juegos de azar y la utilización de estrategias como la exploración de sistemas de datos, la simulación de experimentos y la realización de conteos.
Solución de problemas y modelación	Definida por dos procesos distintos, pero que comparten “el poner en juego ciertas estrategias”, ya sea para hacer una representación simplificada de un fenómeno a través de ecuaciones, funciones o fórmulas o bien para utilizar esta simplificación en la comprensión y resolución de problemas. Dota de recursos para solucionar problemas y plantear modelos, desde una perspectiva global, estos recursos son útiles para comprender el problema, diseñar y ejecutar un plan y probar el resultado. Con estos recursos se resuelven situaciones problemáticas con matemática, se ilustran con modelos realizados con el apoyo de aplicaciones digitales para el aprendizaje, se desarrollan procedimientos de solución tanto formales como intuitivos, estructurados y disruptivos y finalmente a través de detectar la posibilidad de llegar a resultados o la inviabilidad de éstos, se valora a la matemática en diferentes momentos del proceso.	Uso de módulos	Emplear una representación abstracta, conceptual, gráfica o simbólica de un fenómeno o de un proceso para analizar la relación entre sus variables lo que permite comprender fenómenos naturales, sociales, físicos y otros y además, resolver problemas.
		Construcción de modelos	Es un esquema extraído de situaciones problemáticas o de un fenómeno de un contexto específico basado en relaciones, patrones, para elaborar una expresión denominada modelo matemático, esto puede hacerse a partir de una representación gráfica o algebraica donde se describa la situación ya sea real o hipotética.
		Estrategias heurísticas y procesos no rutinarios	La heurística se refiere a estrategias, métodos, criterios o astucias utilizados para hacer posible la solución de problemas complejos. Un procedimiento es no rutinario cuando no basta con aplicar una regla o un método mecanizado o de carácter algorítmico o establecido, sino que requiere cierta intuición y búsqueda poniendo en práctica un conjunto de conocimientos y de experiencias anteriores.
Interacción y lenguaje matemático	Entendida como un proceso social en el que se favorecen la negociación de significados, el consenso, el diálogo y el debate, además de las acciones asociadas con el desarrollo del pensamiento matemático, como la elaboración de conjeturas y argumentos o con la creatividad presente en diversas manifestaciones artísticas y culturales. Tales interacciones deben llegar a expresar las ideas a través del lenguaje matemático para hablar de relaciones o para la construcción de ideas de objetos matemáticos, tales como: incógnita, ecuación, fórmula, etc. con el que se representan las situaciones problema donde, a diferencia del lenguaje natural, se tiene cierto rigor y formalismo. Aporta al individuo recursos para emplear el lenguaje matemático y para interactuar con personas de su entorno dando una dimensión social al aprendizaje.	Registro escrito simbólico-algebraico iconográfico	Revisión de la forma en que se establecen jerarquías, agrupaciones, composiciones en proposiciones, uso formal de símbolos e imágenes respetando las propiedades y reglas.
		Negociación de significados	Revisión colectiva de los significados de las expresiones, dar sentido e interpretar, así como la generación de expresiones y representaciones formales.
		Ambiente matemático de comunicación	Se describe así al ambiente generado por las formas expresivas y evocativas, el uso de figuras, tablas donde se considera lo aprendido y lo conocido en el pasado.

Articulación de Elementos

Los elementos curriculares de Pensamiento Matemático se articulan de la siguiente manera:

Categoría	Subcategorías	Aprendizaje de Trayectoria	Metas de Aprendizaje	Semestre
C1. Procedural	S1.1. Pensamiento aritmético S1.2. Pensamiento algebraico S1.3. Elementos geométricos S1.4. Manejo de datos e incertidumbre	AT1. Valora la aplicación de procedimientos automáticos y de algoritmos para anticipar, encontrar y validar soluciones a problemas (matemáticos, de las ciencias naturales, experimentales y tecnología, sociales, humanidades y de la vida cotidiana).	M1.1. Ejecuta cálculos y algoritmos para resolver problemas matemáticos y de otras áreas del conocimiento.	1° Semestre 2° Semestre 3° Semestre
			M1.2. Analiza los resultados obtenidos al aplicar procedimientos algorítmicos propios del Pensamiento Matemático en la resolución de problemáticas teóricas y de su contexto.	1° Semestre 2° Semestre 3° Semestre
			M1.3. Comprueba los procedimientos usados en la resolución de problemas matemáticos y de otras áreas del conocimiento, mediante la verificación directa o empleando recursos tecnológicos o la interacción con sus pares.	1° Semestre 2° Semestre 3° Semestre
C2. Procesos de intuición y razonamiento	S2.1. Procesos cognitivos S2.2. Pensamiento espacial y razonamiento virtual S2.3. Pensamiento aleatorio	AT2. Adapta procesos de razonamiento matemático que permiten relacionar información y obtener conclusiones de problemas (matemáticos, de las ciencias naturales, experimentales y tecnología, sociales, humanidades, y de la vida cotidiana).	M2.1. Observa y obtiene información de una situación o fenómeno (natural o social) para establecer estrategias o formas de visualización que ayuden a explicarlo.	1° Semestre 2° Semestre 3° Semestre
			M2.2. Desarrolla la percepción y la intuición para generar una hipótesis inicial ante situaciones que requieren explicación o interpretación.	1° Semestre 2° Semestre 3° Semestre
			M2.3. Compara hechos, opiniones o afirmaciones categóricas o la posibilidad de ocurrencia de eventos para establecer similitudes y diferencias, organizándolos en formas lógicas o convenientes útiles en la solución de problemas.	1° Semestre 2° Semestre 3° Semestre
			M2.4. Combina diferentes procesos de razonamiento matemático al plantear un modelo o resolver un problema o una situación o fenómeno natural, experimental o social e interpreta el resultado, la predicción y/o la manera de reducir el nivel de riesgo.	1° Semestre 2° Semestre 3° Semestre
C3. Solución de problemas de modelación	S3.1. Uso de módulos S3.2. Construcción de modelos S3.3. Estrategias heurísticas y procesos no rutinarios	AT3. Modela y propone soluciones a problemas (matemáticos, de las ciencias naturales, experimentales y tecnología, sociales, humanidades y de la vida cotidiana) empleando lenguaje y técnicas matemáticas.	M3.1. Selecciona un modelo matemático por la pertinencia de sus variables y relaciones para explicar el fenómeno estudiado en la solución de un problema.	1° Semestre 2° Semestre 3° Semestre
			M3.2. Construye un modelo con lenguaje matemático y pone a prueba su utilidad para el estudio de un fenómeno (natural o social) o una situación problema.	1° Semestre 2° Semestre 3° Semestre
			M3.3. Aplica procedimientos, técnicas y lenguaje matemático para la solución de problemas propios del Pensamiento Matemático, de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno.	1° Semestre 2° Semestre 3° Semestre
			M3.4. Construye y plantea posibles soluciones a problemas de Áreas de Conocimiento, Recursos Sociocognitivos, Recursos Socioemocionales y de su entorno, empleando técnicas y lenguaje matemático.	1° Semestre 2° Semestre 3° Semestre
C4. Interacción y lenguaje matemático	S4.1. Registro escrito simbólico-algebraico iconográfico S4.2. Negociación de significados S4.3. Ambiente matemático de comunicación	AT4. Explica la solución de problemas en el contexto que le dio origen, empleando lenguaje matemático y lo valora como relevante y cercano a su vida.	M4.1. Describe con sus pares sus conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno.	1° Semestre 2° Semestre 3° Semestre
			M4.2. Socializa con sus pares conjeturas, descubrimientos o procesos en la solución de un problema tanto teórico como de su entorno.	1° Semestre 2° Semestre 3° Semestre
			M4.3. Organiza los procedimientos empleados en la solución de un problema a través de argumentos formales para someterlo a debate o a evaluación.	2° Semestre 3° Semestre

Progresiones de Aprendizaje

Las progresiones de aprendizaje de Pensamiento Matemático están dividas según la UAC a la que pertenecen:

1° Semestre - Progresiones de Aprendizaje - Pensamiento Matemático

2° Semestre - Progresiones de Aprendizaje - Pensamiento Matemático

3° Semestre - Progresiones de Aprendizaje - Pensamiento Matemático

Transversalidad

La transversalidad entre Pensamiento Matemático y los demás recursos y áreas se plantea de la siguiente manera:

Ámbitos de transversalidad con Pensamiento Matemático
Recursos Sociocognitivos	Lengua y Comunicación (e Inglés)	Lengua y Comunicación Los lenguajes naturales (español, lenguas originarias, inglés, etc.) son uno de los principales medios por los que trasmitimos nuestras ideas, y las ideas matemáticas no son la excepción, pero es importante destacar que en la expresión de dichas ideas conviven dos lenguajes, a saber, el formal y el natural, es fundamental que las y los estudiantes manejen ambos correctamente y conozcan sus similitudes y diferencias. Por otro lado, algunos elementos de los lenguajes naturales son susceptibles de ser modelados o descritos a través del uso de, por ejemplo, el pensamiento estadístico y probabilístico. Lengua extranjera: Inglés El lenguaje natural en el que mayoritariamente se comunica la ciencia en la actualidad es el inglés. En ese sentido, es importante ir apuntalando su desarrollo desde estas primeras etapas.
	Cultura Digital	En la actualidad, siempre que sea posible, es recomendable hacer uso de la tecnología para la revisión de algunos contenidos propios del Pensamiento Matemático. Por ejemplo, el uso de simulaciones que permitan modelar el comportamiento de un fenómeno aleatorio posibilitan concretizar algunos elementos del pensamiento estadístico y probabilístico; el uso de software propio de la geometría dinámica permite a las y los estudiantes observar posibles relaciones que han de materializarse en conjeturas que son susceptibles de ser demostradas o refutadas; por último, el uso de programas computacionales que describen las trayectorias y el movimiento de objetos resultan de utilidad en el abordaje del pensamiento variacional.
	Conciencia Histórica	La matemática no está terminada ni mucho menos ha aparecido de la nada. Para comprender al Pensamiento Matemático en su complejidad es necesario conocer la historia de su desarrollo y las motivaciones que han dado origen a algunos de los conceptos más importantes empleados por el Pensamiento Matemático.
Área del Conocimiento	Ciencias Naturales, Experimentales y Tecnología	El lenguaje con el que describimos la naturaleza es el lenguaje matemático. De momento la mejor forma que tenemos para pensar en nuestra realidad física e incluso transformarla es empleando técnicas y contenidos propios de la matemática y el Pensamiento Matemático. El pensamiento estadístico y probabilístico apoya a CNEyT en el estudio de los ecosistemas; el pensamiento aritmético, algebraico y geométrico es fundamental para entender la manera en que se dan algunas reacciones químicas; el pensamiento variacional es el ingrediente principal con el que están descritas las leyes físicas que gobiernan al universo.
	Ciencias Sociales	Las Ciencias Sociales se apoyan del Pensamiento Matemático al hacer uso del pensamiento estadístico, el cual les permite comprender algunos aspectos de fenómenos sociales: las estadísticas son fundamentales para que como colectividad tomemos decisiones razonadas (epidemiología, determinación de presupuesto público, políticas públicas para la reducción de índices de violencia, etc.) Por otro lado, el pensamiento algebraico y el pensamiento variacional dan lugar a que en las Ciencias Sociales se explore el uso de modelos matemáticos para la descripción de fenómenos macro y microeconómicos, el estudio matemático de la dinámica de poblaciones, entre muchos otros fenómenos sociales que deben ser explicados con la metodología y perspectiva propia de las Ciencias Sociales.
	Humanidades	La matemática es un producto del ser humano y la historia del Pensamiento Matemático se desarrolla impulsada por necesidades genuinas que han llevado a matemáticas y matemáticos a crear conceptos que resultaron fundamentales para la humanidad. ¿Cómo se veía e interpretaba la realidad antes del trabajo de Galileo? ¿Cómo entendían la incertidumbre los seres humanos antes de que se formalizara el concepto de azar, aleatoriedad y probabilidad? ¿Qué problemas llevaron a la humanidad al desarrollo de lenguajes formales rigurosos? Estas son tan solo algunas preguntas que pueden abordarse desde las Humanidades y cuya reflexión pudiera arrojar alguna luz sobre la naturaleza del Pensamiento Matemático.
Recursos Socioemocionales	Cuidado Físico-Corporal	Nuestro cuerpo es un sistema complejo y para entenderlo debemos hacer uso de múltiples recursos y considerar aspectos socioemocionales. El Pensamiento Matemático pude apoyar en esta importante labor al, por poner solo un ejemplo, ayudarnos a comprender la dinámica con la que se eliminan sustancias de nuestro cuerpo y los efectos que dichas sustancias provocan en él.
	Bienestar Emocional-Afectivo	Históricamente la matemática y el pensamiento matemático ha sufrido de una cierta resistencia por parte de las y los estudiantes, reconocer esto es el primer paso para la búsqueda de posibles soluciones: la propuesta del MCCEMS reconoce a la matemática como algo vivo en desarrollo que debe ser enseñada con perspectiva socioemocional. El Pensamiento Matemático y las artes han tenido, a lo largo de los años, una íntima relación y comparten conexiones que las y los estudiantes pueden explorar. Se concibe al Pensamiento Matemático como un recurso desde el que se desarrolla la imaginación, la intuición y el descubrimiento intelectual.
	Responsabilidad Social	El Pensamiento Matemático puede aportar posibles rutas de solución a los problemas que aquejan a nuestra comunidad. La contaminación de un río, la movilidad en una ciudad, migración: son estas solo algunas de las problemáticas que pueden interesar a una comunidad y de las que se puede reflexionar desde Pensamiento Matemático en conjunto con otras Áreas y Recursos del MCCEMS.